20221230@二叉树数据结构的应用

树型结构（Tree）是一种重要的非线性数据结构，它为计算机应用中出现的具有层次关系的数据提供了一种有效的表示方法，比如文件目录结构、源程序语法结构等。

# 树的定义和基本术语
树是 n(n>=0) 个节点的有限集合 T。在任意一棵非空树中满足如下两个条件：
- 有且仅有一个根节点（Root）。
- 当 n>1 时，其余节点可分为 m(m>=0) 个互不相交的有限集合 T1，T2，……，Tm，其中每一个集合本身又都是一棵树，并且称为根的子树（Subtree），如下图所示。

# 树型结构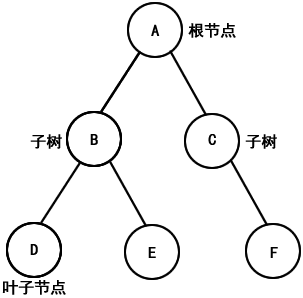

![](/media/202212/2022-12-30_141011_2118450.8678622304047892.png)
图：树型结构

由上图可知，树的定义是递归的，树是一种递归数据结构。树的这种定义为树的递归处理带来了很大方便，本节举例中几乎所有对树的处理都采用了递归算法。

>在了解树型结构时，还有几个基本概念非常重要，必须要掌握：
>- 节点的度：树中每个节点具有的子树数，或后继节点数称为该节点的度。
>- 树的度：树中所有节点的度的最大值称为树的度。
>- 分支节点：度大于 0 的节点称为分支节点或非终端节点。
>- 叶子节点：度为 0 的节点称为叶子节点或终端节点。
>- 儿子节点：一个节点的后继称为该节点的儿子节点。
>- 父亲节点：一个节点称为其后继节点的父亲节点。
>- 子孙节点：一个节点的所有子树中的节点称为该节点的子孙节点。
>- 祖先节点：从根节点到达一个节点的路径上，通过的所有节点称为该节点的祖先节点。
>- 兄弟节点：具有同一父亲的节点相互称为兄弟节点。
>- 节点的层数：树是一种层次结构，根节点为第一层，其儿子节点为第二层，以此类推可以得到每个节点的层数。
>- 树的深度：树中节点的最大层数称为树的深度或高度。
>- 森林：0个或多个不相交的树的集合称为森林。

# 二叉树简介
二叉树是一种特殊的树，具有如下特点：
- 二叉树中每个节点最多有两棵子树，称为左子树、右子树；
- 左子树和右子树是有顺序的，有左右之分，次序不能随意颠倒；
- 即使某个节点只有一个子树，也要区分左右子树。

除了这些基本特征外，还有如下一些特殊的二叉树。
**1) 斜树**
所有的节点只有左子树则称为左斜树；所有节点只有右子树则称为右斜树。如下图所示：

左斜树和右斜树
![](/media/202212/2022-12-30_141224_8943100.8055018761669762.png)
图：左斜树和右斜树

**2) 满二叉树**
在一棵二叉树中，所有的分支结点都存在左子树和右子树，并且所有的叶子结点都在同一层上，这样的二叉树称为满二叉树。就是完美圆满的意思。

![](/media/202212/2022-12-30_141304_8578650.14551105995332225.png)
图：满二叉树

满二叉树的特点如下所示：
- 叶子只能出现在最下一层。
- 非叶子结点度一定是 2.
- 在同样深度的二叉树中，满二叉树的结点个数最多，叶子树最多。

**3) 完全二叉树**
在一棵二叉树中，除最后一层外，若其余各层都是满的，最后一层要么是满的，要么在右边缺少若干个连续的节点，这样的二叉树被称为完全二叉树。满二叉树必须是完全二叉树，而完全二叉树不一定是满二叉树。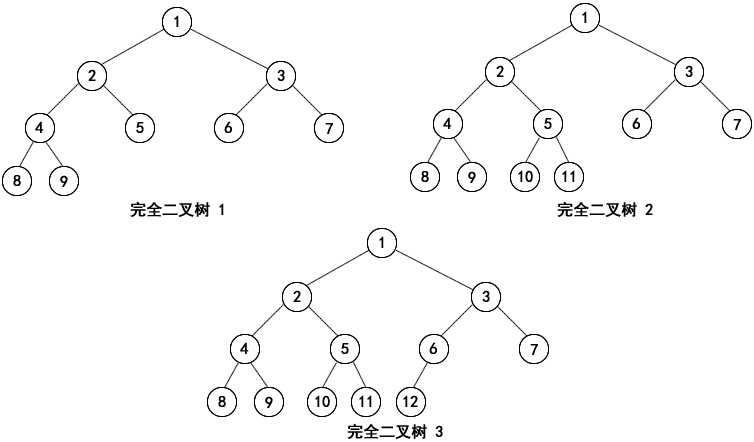

![](/media/202212/2022-12-30_141345_8350360.06219378800332254.png)
图：完全二叉树

完全二叉树的特点如下所示：
- 叶子结点只能出现在最下一层（满二叉树继承而来）。
- 最下层叶子结点一定集中在左部连续位置。
- 倒数第二层，如有叶子节点，一定出现在右部连续位置。
- 同样结点树的二叉树，完全二叉树的深度最小。

# 二叉树的链接存储结构
二叉树的存储方法有
- 顺序存储
- 链接存储
- 线索树存储
其中，顺序存储是使用数组来完成，而链接存储和线索树存储都使用了链表来完成。本节在二叉树的应用举例中使用了链接存储法。

## 节点定义
在二叉树的链接存储结构中，通常采用的方法是：每个节点设置三个域，即值域、左指针域和右指针域，其结构如下图所示。

![](/media/202212/2022-12-30_141456_8585620.8613504210129707.png)
图：二叉树链接存储结构

其中 Data 表示值域，用于存储放入节点中的数据元素，LeftChild 和 RightChild 分别表示左指针域和右指针域，用以分别存储左子树和右子树节点的指针地址。

链接存储的指针类型和节点定义如下：
```go
type Node struct {
    Left *Node
    Data interface{}
    Right *Node
}
```

这里的 Data 字段可以是任意基本数据类型，如 int、float、string 等。链表所有节点的 Data 字段类型一致，比如同为 int 型或同为 string 型。在本节的应用举例中，二叉树节点的 Data 字段将被设置成空接口 interface{}，这样二叉树的叶子节点将能够存储不同类型的数据，比如一个节点为 int 型，其他节点可以为 string 型等。

## 接口定义
二叉树的应用处理功能主要包括：
- 二叉树新节点的创建、初始化；
- 二叉树的输出、度的计算、叶子节点统计等基本操作；
- 二叉树的前序、中序、后序遍历等。

针对这些功能本例共定义了三个接口：Initer、Operater 和 Order。
### 1) Initer 接口
当为二叉树创建了一个新节点时，Initer 接口提供了 SetData() 方法可以对节点的 Data 字段进行初始化。
```go
Initer 接口定义如下：
type Initer interface {
    SetData (data interface{})
}
```
### 2) Operater 接口
当已经生成了一个二叉树时，可以使用 Operater 接口提供的三个方法：PrintBT()、Depth() 和 LeafCount()，对二叉树进行输出、深度计算和叶子统计等基本操作。

Operater 接口定义如下：
```go
type Operater interface {
    PrintBT()
    Depth() int
    LeafCount() int
}
```

### 3) Order 接口
对二叉树的遍历是一个重要的功能，这些功能在接口 Order 中实现，Order 接口中共定义了三个方法，分别是 PreOrder()、InOrder() 和 PostOrder()，分别可以实现前序遍历、中序遍历和后序遍历。

Order 接口的定义如下：
```go
type Order interface {
    PreOrder()
    InOrder()
    PostOrder()
}
```
可以看到，在定义接口时，接口中的方法只需声明原型，而并不需在此实现。这些方法的实现可以在其他 Go 包文件中实现，或者直接由其他用户提供。

接口的意义也在于此，即同一个接口可以有不同的实现方式，甚至由不同的人去完成。

## 方法的实现
通过接口的概念知道接口是方法的组合，而在定义接口时不必马上实现方法，方法可由设计者自己或交由其他人单独设计。本例三个接口中共有 7 个方法，下面分别介绍一下它们是怎么实现的。
### 1) SetData 方法
SetData() 通过空接口 interface{}，可以将任意类型数据赋值给二叉树节点的 Data 字段，实现二叉树对任意数据类型的存储。
```go
SetData 方法的定义如下：
func (n *Node) SetData(data interface{}) {
    n.Data = data
}
```

### 2) PrintBT 方法
PrintBT() 调用底层函数 PrintBT()，输出一个给定二叉树的嵌套括号表示。

PrintBT 方法的定义如下：
```go
func (n *Node) PrintBT() {
    PrintBT(n)
}
```
### 3) Depth 方法
Depth() 调用底层函数 Depth()，返回二叉树的深度。

Depth 方法的定义如下：
```go
func (n *Node) Depth() int {
    return Depth(n)
}
```

### 4) LeafCount 方法
LeafCount() 调用底层函数 LeafCount()，返回二叉树的叶子节点数。

LeafCount 方法的定义如下：
```go
func (n *Node) LeafCount() int {
    return LeafCount(n)
}
```

### 5) PreOrder 方法
PreOrder() 调用底层函数 PreOrder() 对二叉树进行前序遍历。

PreOrder 方法的定义如下：
```go
func (n *Node) PreOrder() {
    PreOrder(n)
}
```

### 6) InOrder 方法
InOrder() 调用底层函数 InOrder() 对二叉树进行中序遍历。

InOrder 方法的定义如下：
```go
func (n *Node) InOrder() {
    InOrder(n)
}
```

### 7) PostOrder 方法
PostOrder() 调用底层函数 PostOrder() 对二叉树进行后序遍历。

PostOrder 方法的定义如下：
```go
func (n *Node) PostOrder() {
    PostOrder(n)
}
```

# 底层函数设计
在面向对象程序设计中，上层方法的功能实现还要依赖底层函数，本例中大部分方法也是这样，现将所有底层函数一一列举如下。
## 1) NewNode 函数
NewNode() 按照链接存储方式生成一个新的二叉树节点，参数 left 指向左指针域，参数 right 指向右指针域。

NewNode 函数的定义如下：
```go
func NewNode(left, right *Node) *Node {
    return &Node{left, nil, right}
}
```

## 2) PrintBT 函数
PrintBT() 用于输出一个给定二叉树的嵌套括号表示，采用递归算法：
首先输出根节点，然后再依次输出左子树和右子树，在输出左子树前打印输出左括号“(”，在输出右子树后打印输出右括号“)”；
另外，依次输出的左、右子树要至少有一个不为空，若都为空就不必输出了。

PrintBT 函数的定义如下：
```go
func PrintBT(n *Node) {
    if n != nil {
        fmt.Printf("%v", n.Data)
        if n.Left != nil || n.Right != nil {
            fmt.Printf("(")
            PrintBT(n.Left)
            if n.Right != nil {
                fmt.Printf(",")
            }
            PrintBT(n.Right)
            fmt.Printf(")")
        }
    }
}
```

## 3) Depth 函数
Depth() 用于计算二叉树的深度，采用递归算法：
若一棵二叉树为空，则其深度为 0；
否则，其深度等于左子树或右子树的最大深度加 1。

Depth 函数的定义如下：
```go
func Depth(n *Node) int {
    var depleft, depright int
    if n == nil {
        return 0
    } else {
        depleft = Depth(n.Left)
        depright = Depth(n.Right)
        if depleft > depright {
            return depleft + 1
        } else {
            return depright + 1
        }
    }
}
```

## 4) LeafCount 函数
LeafCount() 用于统计二叉树叶子节点数，采用递归算法：
若一棵二叉树为空，则其叶子节点数为 0；
若一棵二叉树的左、右子树均为空，则其叶子节点数为 1；
否则叶子数等于左子树与右子树叶子总数之和。

LeafCount 函数的定义如下：
```go
func LeafCount(n *Node) int {
    if n == nil {
        return 0
    } else if (n.Left == nil) && (n.Right == nil) {
        return 1
    } else {
        return (LeafCount(n.Left) + LeafCount(n.Right))
    }
}
```
## 5) PreOrder 函数
PreOrder() 可以对二叉树进行前序遍历，采用递归算法，按照先访问根节点，再访问左子树，最后访问右子树的次序访问二叉树中的所有节点，且每个节点仅访问一次。

PreOrder 函数的定义如下：
```go
func PreOrder(n *Node) {
    if n != nil {
        fmt.Printf("%v", n.Data)
        PreOrder(n.Left)
        PreOrder(n.Right)
    }
}
```

## 6) InOrder 函数
InOrder() 可以对二叉树进行中序遍历，采用递归算法，按照先访问左子树，再访问根节点，最后访问右子树的次序访问二叉树中的所有节点，且每个节点仅访问一次。

InOrder 函数的定义如下：
```go
func InOrder(n *Node) {
    if n != nil {
        PreOrder(n.Left)
        fmt.Printf("%v", n.Data)
        PreOrder(n.Right)
    }
}
```

## 7) PostOrder 函数
PostOrder() 可以对二叉树进行后序遍历，采用递归算法，按照先访问左子树，再访问右子树，最后访问根节点的次序访问二叉树中的所有节点，且每个节点仅访问一次。

PostOrder 函数的定义如下：
```go
func PostOrder(n *Node) {
    PreOrder(n.Left)
    PreOrder(n.Right)
    fmt.Printf("%v", n.Data)
}
```

# 二叉树基本应用测试
前面介绍了二叉树链接存储结构，以及节点定义、接口定义、方法实现和底层函数设计，并在包 btree 中实现。接下来将利用这些知识实现几个二叉树的基本应用，包括二叉树的创建、基本操作和遍历。

## 二叉树创建
二叉树的创建过程一般如下：
首先调用 NewNode() 函数创建根节点，再调用 SetData() 方法初始化根节点。
使用同样的方法创建左子树和右子树，并将左、右子树链接到根节点上。
如果左、右子树有叶子节点，则插入叶子节点并和左、右子树建立链接。

【示例 1】二叉树的建立，本例将演示如何使用 Initer 接口实现根节点的初始化。
```go
// 二叉树的建立
package main
import(
    "fmt"
    "btree"
)
func main() {
    //创建根节点
    root := NewNode(nil, nil)
    var it Initer
    it = root
    it.SetData("root node")
    //创建左子树
    a := NewNode(nil, nil)
    a.SetData("left node")
    al := NewNode(nil, nil)     //左叶子节点
    al.SetData(100)
    ar := NewNode(nil, nil)     //右叶子节点
    ar.SetData(3.14)
    a.Left = al
    a.Right = ar
    //创建右子树
    b := NewNode(nil, nil)
    b.SetData("right node")
    root.Left = a
    root.Right = b
    root.PrintBT()
}
```
编译并运行该程序，输出结果为：
```
root node (left node ( 100,3.14 ),right node)
```

通过输出结果可以看出，在示例中首先创建了根节点 root node，然后创建左子树 left node 和右子树 right node。左子树有两个叶子节点，左叶子的值为 int 型 "100"，右叶子的值为 float 型 "3.14"。即该二叉树可以存储不同类型的值，这些都是由空接口 interface{} 实现的。

## 二叉树基本操作
对一个已存在的二叉树的基本操作包括二叉树的输出、深度计算、叶子数统计等，在下面将演示如何使用 Operater 接口实现这些基本操作。

【示例 2】二叉树的基本操作。
```go
// 二叉树的基本操作
package main
import(
    "fmt"
    "btree"
)
func main() {
    //创建二叉树
    root := NewNode(nil, nil)
    root.SetData("root node")
    a := NewNode(nil, nil)
    a.SetData("left node")
    al := NewNode(nil, nil)
    al.SetData(100)
    ar := NewNode(nil, nil)
    ar.SetData(3.14)
    a.Left = al
    a.Right = ar
    b := NewNode(nil, nil)
    b.SetData("right node")
    root.Left = a
    root.Right = b
    // 使用 Operater 接口实现对二叉树的基本操作
    var it Operater
    it = root
    it.PrintBT()
    fmt.Println()
    fmt.Println("The depths of the Btree is:", it.Depth())
    fmt.Println("The leaf counts of the Btree is:", it.LeafCount())
}
```
编译并运行该程序，输出结果为：
```
root node ( left node (100,3.14),right node )
The depths of the Btree is: 3
The leaf counts of the Btree is: 3
```

通过输出结果可以看出，上面示例中二叉树的深度为 3，叶子节点数也为 3，这和验证结果完全一致。另外，对二叉树的操作还有査找、插入、删除节点等，大家可以在上面的基础上自行完成。

## 二叉树遍历
在二叉树的一些基本应用中，常常需要在树中查找具有某种特征的节点，或者对树中全部节点逐一进行某种处理，这就是二叉树的遍历（Traversing binary tree）。即如何按某条搜索路径访问树中的每个节点，使得每个节点均能被访问一次，而且仅被访问一次。

二叉树的遍历方法一般分为前序遍历、中序遍历和后序遍历，下面示例将演示如何使用 Order 接口实现二叉树的三种遍历。

【示例 3】二叉树的遍历。
```go
// 二叉树的遍历
package main
import(
    "fmt"
    "btree"
)
func main() {
    //创建二叉树
    root := NewNode(nil, nil)
    root.SetData("root node")
    a := NewNode(nil, nil)
    a.SetData("left node")
    al := NewNode(nil, nil)
    al.SetData(100)
    ar := NewNode(nil, nil)
    ar.SetData(3.14)
    a.Left = al
    a.Right = ar
    b := NewNode(nil, nil)
    b.SetData("right node")
    root.Left = a
    root.Right = b
    // 使用 Order 接口实现对二叉树的基本操作
    var it Order
    it = root
    it.PreOrder()       //先序遍历
    fmt.Println()
    it.InOrder()        //中序遍历
    fmt.Println()
    it.PostOrder()      //后序遍历
}
```

编译并运行该程序，输出结果为：
```
root node left node 100 3.14 right node
left node 100 3.14 root node right node
left node 100 3.14 right node root node
```

通过输出结果可以看出，示例的三种遍历方法输出结果和验证结果完全一致。当然在对二叉树进行遍历的同时，用户也可以对树中的节点做各种处理，比如修改节点信息等。